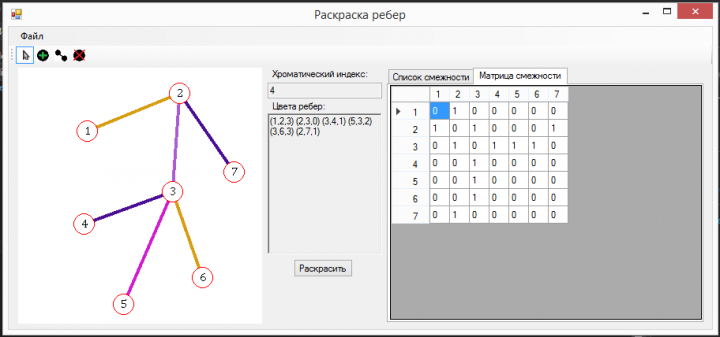
Раскраска ребер

Научная визуализация
Граф называется k -реберно-раскрашиваемым , если существует правильная раскраска ребер вkцветов. Пусть fбудет функцией, которая присваивает цвета ребрам графа. Проблема нахождения f-раскраски ребер графа являетсяNP-тяжелой, а нахождениеf-хроматического индекса —NP-сложной. Совершенным графом aperfectgraph является граф, у которого хроматическое число каждого наведенного подграфа равно числу клики этого подграфа. Так, если каждый наведенный подграф имеет по меньшей мереkвершин, то совершенный граф может быть раскрашен вkцветов вершинная раскраска. Для всех совершенных графов решение проблем нахождения максимальной клики, максимального независимого множества, а также правильной раскраски вершин может быть найдено в полиномиальное время.




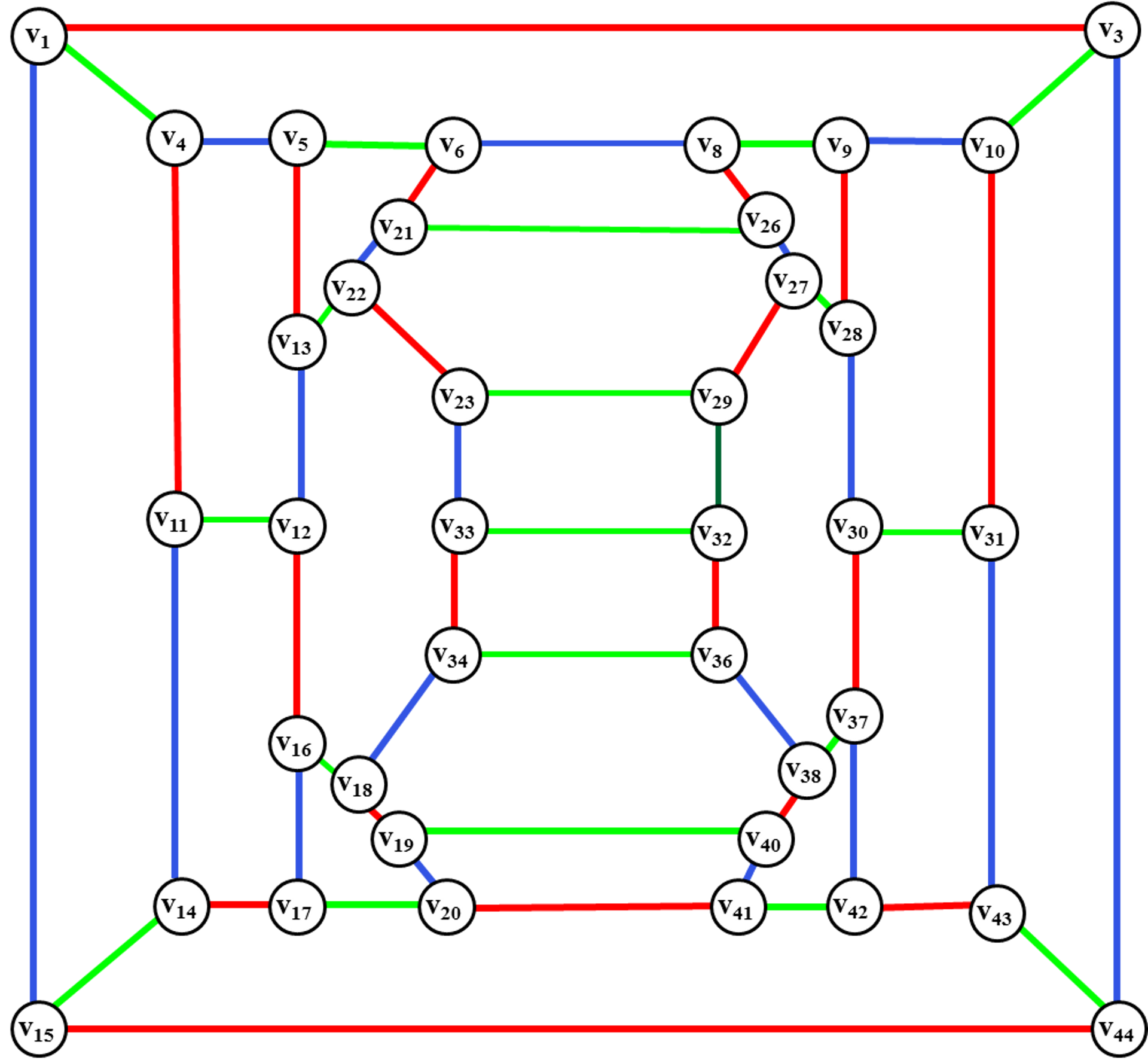

Предписанная раскраска рёбер графа — это вид раскраски графов , в которой комбинируется предписанная раскраска и раскраска ребер. Предписанная раскраска — это вид раскраски графов, в которой каждая вершина может принимать ограниченное множество допустимых цветов. Раскраска ребер — назначение «цветов» рёбрам графа таким образом, что смежные ребра имеют разный цвет.





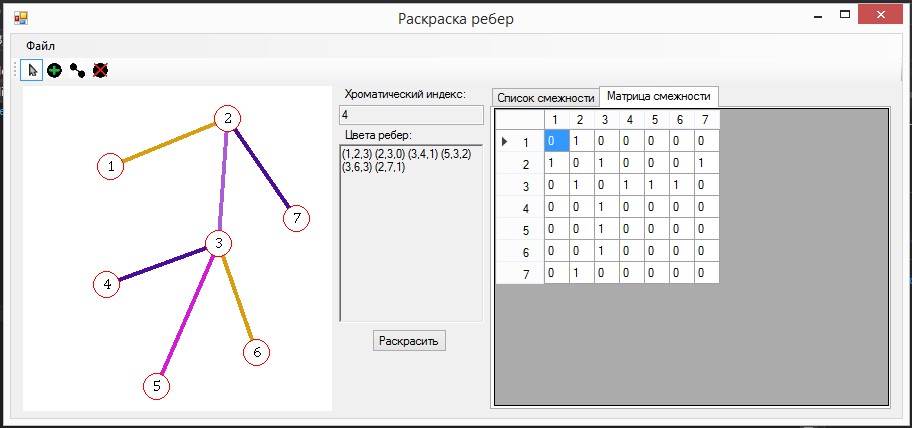
| 404 | Каждому подмножеству сопоставляется краска, в которую окрашиваются все ребра этого подмножества. | |
| 482 | В этой небольшой заметке я хочу показать, как с помощью алгебры можно решать классическую задачу о раскраске вершин графа. | |
| 268 | Все сервисы Хабра. | |
| 436 | Раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета - это числа. | |
| 212 | Алгоритм раскраски рёбер Мисры и Гриса — это алгоритм полиномиального времени в теории графов , который находит рёберную раскраску любого графа. | |
| 438 | RU доступ к данной странице для анонимных пользователей с IP-адреса |
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается. Цвета — это целые положительные цифры. Графы нужно раскрашивать так, чтобы соседние вершины имели разные цвета. Еще стоит использовать как можно меньше цветов. Первый пример на схеме выше не совсем верный, потому что соседним вершинам присваивается один и тот же цвет.